Capítulo 2: Campo, Potencial, Força e Energia
Carlos Alberto dos Santos, Eliabe Maxsuel de Aquino, Geovani Ferreira Barbosa
Universidade Federal Rural do Semi-Árido
Mestrado Nacional Profissional em Ensino de Física
Campo, potencial, força e energia
A essa altura precisamos incluir os conceitos de força e energia, pois você deve ter lido, um pouco mais acima, que a partir da relação do potencial com o campo, chega-se à energia potencial. Mas, para isso é necessário introduzirmos o conceito de força elétrica. Cinquenta anos antes de Faraday criar o conceito de campo elétrico, Charles Augustin de Coulomb descobriu a lei que ficou conhecida como lei de Coulomb, que fornece a força entre duas cargas elétricas, q e Q, a uma distância r entre elas.


Substituindo (2.1) em (2.4), obtém-se

A equação (2.5) expressa o conceito de força por intermédio do campo. Ou seja, a carga Q cria um campo elétrico E, que exerce a força qE sobre a carga q.
Se há uma força sobre uma partícula carregada, essa força vai realizar um trabalho sobre a partícula, ou seja, vai lhe for- necer energia. Embora estejamos falando de carga elétrica, força elétrica e energia elétrica, tudo isso pode ser tratado do mesmo modo como aprendemos com o campo gravitacional e as leis de Newton. É muito instrutivo estabelecermos a relação entre força elétrica, campo elétrico e energia elétrica partindo do que aprendemos na mecânica newtoniana.

Pela lei da gravitação universal de Newton, dois corpos, m e M, separados por uma distância r, atraem-se com uma força dada por:

onde G é a constante gravitacional. Veja que esta fórmula fica igual à (2.4) se substituirmos G por k, m por q e M por Q. Podemos dizer que elas são formalmente iguais. Mais importante do que essa semelhança, é o fato de que as principais propriedades físicas resultantes de (2.6) podem ser estendidas para a lei de Coulomb. Essas forças são conhecidas como forças conservativas porque levam ao teorema da conservação da energia (energia cinética + energia potencial) e ao teorema do trabalho-energia.
Para um sistema conservativo, regido pelas equações (2.4) e (2.6), a energia total é sempre conservada. Ou seja, a soma da variação da energia cinética, ΔEc, com a variação da energia potencial, ΔEp, é zero:
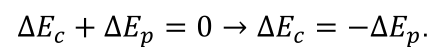
Por outro lado, o trabalho, T, realizado sobre uma partícula num sistema conservativo é sempre igual à variação da energia cinética da partícula:

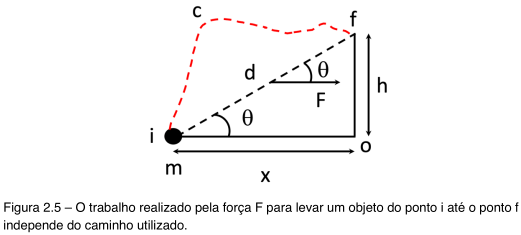
Precisamos agora resolver um problema que você deve ter resolvido quando estudou mecânica. O problema é calcular o trabalho para levar um objeto de massa m, de um ponto i até um ponto f, como ilustrado na figura 2.5. Isso pode ser feito levando o objeto pelo caminho iof, ou pelo caminho d, ou pelo caminho c, ou por qualquer caminho que comece em i e termine em f. Para re- solver o problema precisamos saber como calcular o trabalho de uma força, ao longo de uma trajetória paralela à direção da força. Você aprendeu na mecânica que o trabalho é o produto da força pela distância percorrida.
O trabalho para levar a partícula de i até o ponto o é:

O trabalho para levar a partícula de o até o ponto f é nulo, porque o cami- nho é perpendicular à direção da força. Portanto, o trabalho para levar a partícula pelo caminho iof é dado por (2.8).
Pelo caminho d, o trabalho será:
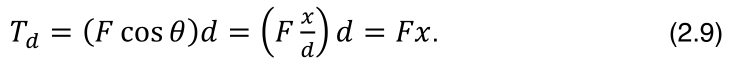
Como (2.8) é igual a (2.9), conclui-se que o trabalho pelo caminho iof é igual ao trabalho pelo caminho d.

Agora temos tudo para relacionar campo elétrico, potencial elétrico e energia potencial. Para evitar confusão, vamos denominar energia potencial pela letra U, em vez de Ep Vamos reescrever a equação (2.7):
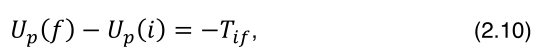
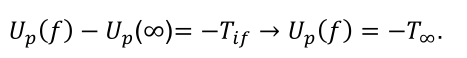
Portanto, dada uma configuração de cargas e uma carga de prova, q0, a energia potencial dessa configuração é o negativo do trabalho realizado pelo campo da configuração para trazer a carga de prova do infinito até o ponto em que ela se encontra.
A situação que discutimos até agora é assim: uma carga elétrica cria um campo elétrico. A intensidade desse campo decresce com o aumento da distância à carga, conforme a equação (2.1). Se uma carga, q, for colocada no campo de ação do campo, ela será submetida a uma força dada pela fórmula (2.5). Essa força realizará trabalho sobre a carga levando-a de um ponto a outro, conforme a fórmula (2.10).
Mas, em vez de trabalhar com energia potencial, é melhor trabalhar com potencial, assim definido:
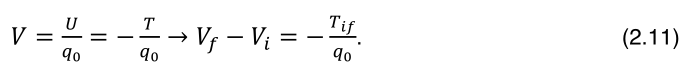
O trabalho realizado por uma força F, do ponto i ao ponto f, ao longo de um percurso x é dado por (2.8):

Substituindo (2.12) em (2.11), obtém-se a expressão para a diferença de potencial (ddp) entre dois pontos, i e f, em função do campo elétrico:
