Capítulo 4: Circuitos Elétricos
Carlos Alberto dos Santos, Eliabe Maxsuel de Aquino, Geovani Ferreira Barbosa
Universidade Federal Rural do Semi-Árido
Mestrado Nacional Profissional em Ensino de Física
Não há praticamente nada em nosso dia a dia que não dependa de pelo menos um circuito elétrico, quase sempre bastante complexo, como essa placa mãe de um computador, similar a este que estou usando para escrever esse texto. Diariamente engenheiros eletricistas dedicam-se aos cálculos de correntes e diferenças de potenciais nesses circuitos, com o objetivo de montar seus projetos e fabricar equipamentos. As conexões entre os vários componentes do circuito são feitas no verso da placa, como na fotografia abaixo.


Até mesmo para tarefas simples, sistemas eletrônicos são fabricados, como essa placa usada para a extração de água de uma bombona caseira.
Para abordar todos esses circuitos elétricos, são necessários basicamente o conheci- mento da lei de Ohm, que você aprendeu no capítulo anterior e das leis de Kirchhoff, que serão abordadas aqui apenas de forma bastante introdutória e qualitativa.
Todo circuito necessita de pelo menos uma bateria ou fonte de tensão para fazê-lo funcionar, e de um ou mais interruptores, que, como o nome sugere, servem para interromper o funcionamento do circuito. Se não fosse assim, as lâmpadas de nossas casas ficariam sempre apagadas ou sempre acesas. Um dos circuitos mais simples que podemos imaginar consiste de uma bateria, um interruptor e uma lâmpada incandescente1.

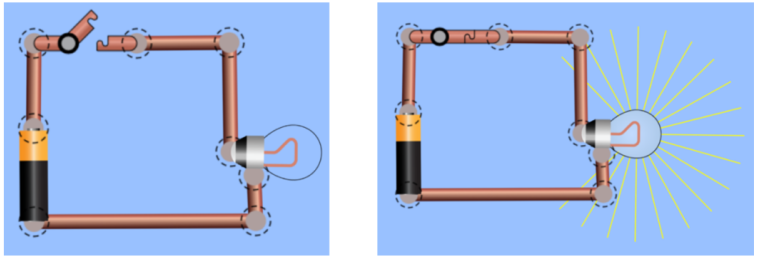
Quando o interruptor é fechado, a lâmpada brilha, ou seja, emite luz. Por quê? Na maioria dos livros didáticos diz-se que isso acontece porque os elétrons na resistência da lâmpada2 atingem altas temperaturas, que os faz emitir luz visível. Isso é parte da verdade, mas não é tudo. Porque o fato de atingir altas temperaturas os faz emitir luz visível? Logo depois da descoberta do elétron, em 1897, Joseph Larmor descobriu que uma partícula carregada em movimento emite luz, cuja frequência é proporcional à sua velocidade. Por outro lado, a temperatura de um corpo também é proporcional à velocidade dos componentes atômicos do corpo. É isso que justifica as afirmações contidas nos livros didáticos, de que os materiais condutores emitem luz por causa das altas temperaturas que apresentam durante a passagem da corrente elétrica.

É inevitável a repetição de ideias, conceitos e leis já abordados, na descrição que faremos aqui do fenômeno da condutividade elétrica em circuitos simples. Aliás, do ponto de vista didático essa repetição é conveniente, pois facilita a internalização dos conceitos abordados.
No momento que o interruptor (chave) é ligado, o campo elétrico produzido pela bateria começa a atuar nas cargas distribuídas ao longo dos condutores do circuito. Assim que um elétron sai do polo negativo da bateria, outro entra pelo polo positivo. Veja que não é o elétron que sai do polo negativo que vai ser absorvido pelo polo positivo. Mas, a quantidade de elétrons que saem do polo negativo da bateria é igual à quantidade que entra no polo positivo. Isso significa que há conservação da carga elétrica no circuito. Nenhuma carga desaparece no processo da condutividade elétrica. O mesmo acontece com a corrente elétrica, que também é conservada. Não há qualquer tipo de consumo da corrente elétrica no circuito.
Então, a corrente que sai da bateria é igual à que entra. A corrente sai da bateria por causa do campo elétrico produzido por ela. A bateria não é fonte de corrente, ela é fonte de tensão, ou de potencial, ou de força eletromotriz. Tudo isso é produzido pelo campo elétrico.
Cada bateria tem uma força eletromotriz (fem) que depende do processo de fabricação. Por exemplo, essas pilhas que costumamos usar em diversos aparelhos domésticos, têm forças eletromotrizes que variam de 1,5 V a 9 V. Com o tempo, o material que produz a força eletromotriz vai sendo consumido até que a pilha deixa de funcionar porque deixa de produzir a voltagem exigida pelos equipamentos.

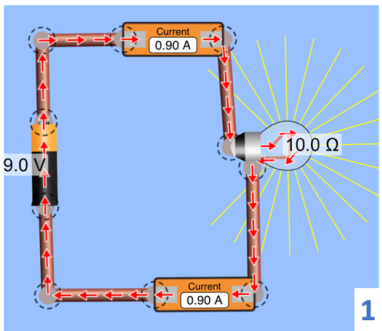
Então, a fem é fixa, mas a corrente que sai de um polo da bateria e entre pelo outro depende do circuito. Veja bem o circuito (1). Uma bateria de 9 V alimenta uma lâmpada de 10 W. As setas vermelhas indicam a corrente convencional, aquela que sai do polo positivo e entra no polo negativo.
Um amperímetro mede a corrente na saída da bateria, e outro mede a corrente na entrada. Como foi dito acima, as duas correntes são iguais. Portanto, a corrente é conservada ao longo do circuito. Embora seja quase universal o uso da corrente convencional, a corrente real é aquela formada pelo fluxo de elétrons livres, saindo do polo negativo no sentido do polo positivo, como ilustra o circuito (2).
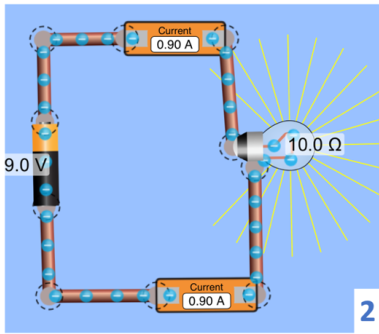
A corrente de 0,9 A medida pelo amperímetro não é uma propriedade da bateria. Ela depende dos componentes do circuito. O que é propriedade da bateria é a fem.
Para verificar que a corrente depende do circuito, vamos acrescentar uma lâmpada, permanecendo com a mesma pilha de 9 V. Veja que a corrente agora é a metade da anterior.
Vamos acrescentar a segunda lâmpada de outro modo.
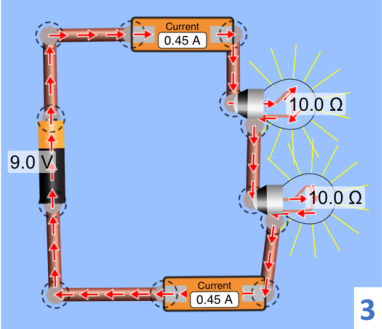
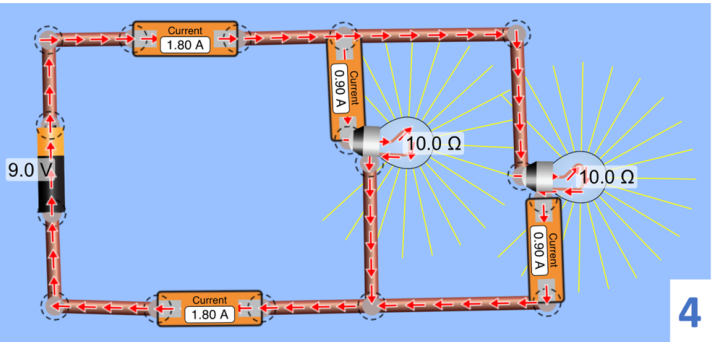
Veja que, em comparação com o circuito (1), a corrente de saída (e de entrada) dobrou o valor, enquanto a corrente que passa em cada lâmpada é a metade da corrente que sai da bateria.
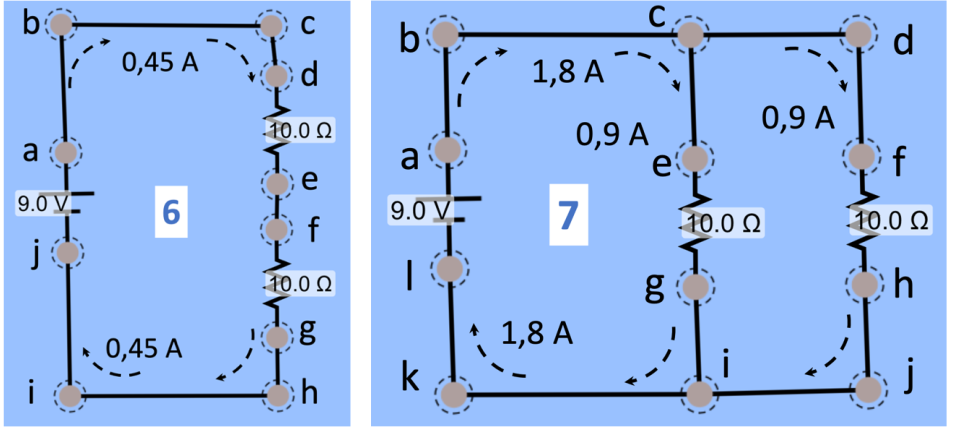
Vamos redesenhar os circuitos (1), (3) e (4) com os símbolos usados nos livros didáticos e discuti-los o mais detalhadamente possível. Agora eles foram renomeados: 5, 6 e 7. Vamos responder as seguintes questões:
- Por que a corrente no circuito 6 é a metade da corrente no circuito 5?
- Por que a corrente de saída e entrada no circuito 7 é o dobro da corrente no circuito 5?
- Por que no circuito 7 as correntes nos trechos c-i e d-j são iguais à metade da corrente de saída?
Tudo isso tem a ver com a lei de Ohm (eq. 3.2), que vamos reescrever na forma como usualmente é apresentada nos livros didáticos:

Na equação (4.1), V representa a diferença de potencial entre as extremidades da resistência. Por comodidade escreve-se V em vez de ΔV. Portanto, quando uma corrente i atravessa um condutor com resistência R, aparece uma diferença de potencial (ddp), V, entre suas extremidades. Vejamos como usamos essa equação nos circuitos elétricos simples.
Tudo que for dito sobre esse circuito poderá ser aplicado nos circuitos 6 e 7. Esse circuito é igual ao circuito 1. Apenas substituímos os símbolos. Tem-se uma bateria ou fonte de tensão de 9 V e um resistência de 10 W. Para montar o circuito, temos que usar fios condutores para conectar os componentes. Esses fios são fabricados de tal modo que suas resistências elétricas são praticamente nulas, comparadas com as resistências dos componentes eletro-eletrônicos. Para esse circuito 5 usamos os fios abcd e efgh. Como indicado no circuito 1, o amperímetro mediu uma corrente de 0,9 A.
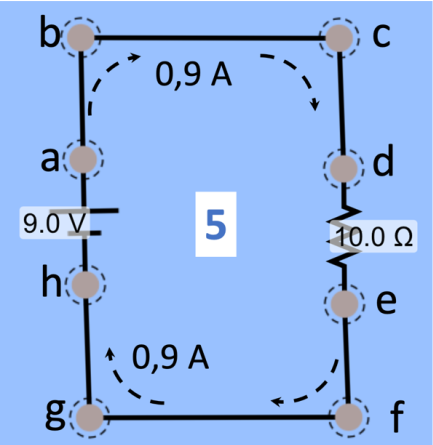
Portanto, só haverá diferença de potencial entre os pontos a e h (ΔV=Va-Vh=9V) e entre d e e, ou seja, através do resistor. Essa ddp (Vd-Ve) será, conforme a equação (4.1), o produto de R (10 Ω) por i (0,9 A), ou seja 9 V, que é exatamente a fem da bateria. Esse resultado foi obtido com a lei de Ohm, mas podemos obtê-lo sem fazer uso dessa lei. Como o fio abcd não tem resistência, o potencial em a é igual ao potencial em d. Da mesma forma, o potencial em h é igual ao potencial em e. Ou seja:
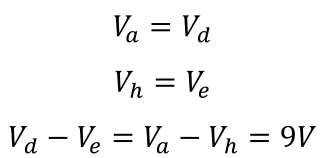
Esse procedimento pode ser aplicado em muitos circuitos, com diferentes associações de resistências. Existem duas formas de associar resistências. Uma delas é o que chamamos de associação em série, como no circuito 6. A outra forma é a associação em paralelo, como no circuito 7. Geralmente os circuitos são contêm os dois tipos de associação, como no circuito 8. Qualquer que seja o tipo de associação, podemos substituir o conjunto das resistências por uma única, que denominamos de resistência equivalente. No presente caso, o circuito 8 é substituído pelo circuito 9, e finalmente o circuito 9 é substituído pelo 10. A resistência R123 é a resistência equivalente das três resistências do circuito 8. Vejamos como calcular R123.
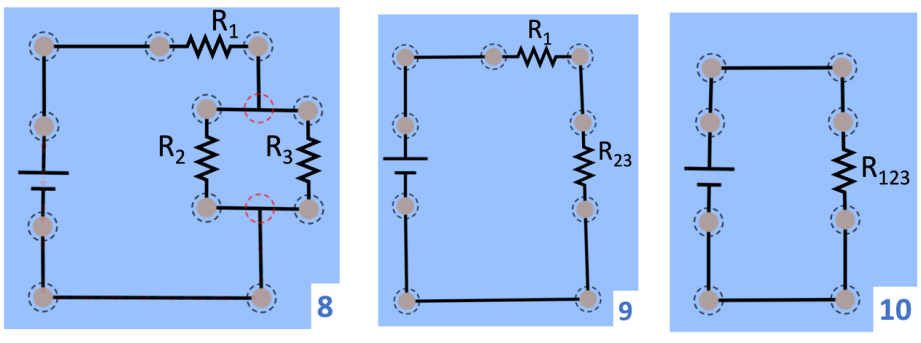
A resistência equivalente de duas ou mais resistências em série é a soma das resistências. O inverso da resistência equivalente de duas ou mais resistências em paralelo é a soma dos inversos das resistências. R23 é a resistência equivalente de R2 e R3, que estão em paralelo:
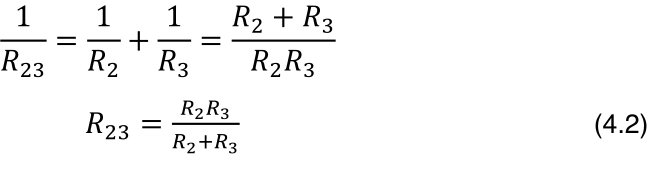
Mostre que a resistência equivalente de três resistências em paralelo é dada pela fórmula:
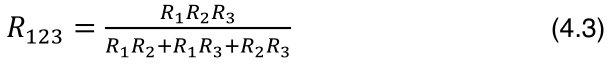
No circuito 9, R1 e R23 estão em série, logo:
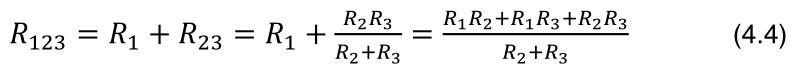
Você pode usar essa sistemática para calcular a resistência equivalente de qualquer circuito simples como esses que estamos tratando aqui, sempre cmeçando do final do circuito para o início. Por exemplo, no circuito 11a você pode calcular a resistência equivalente começando pelas resistências R4 e R5, que estão em paralelo. Calcule R45. Esta está em série com R3. Calcule R345 Esta está em paralelo com R2. Calcule R2345. Finalmente, R2345 está em série com R1, de modo que a resistência equivalente do circuito será Req = R1+R2345.
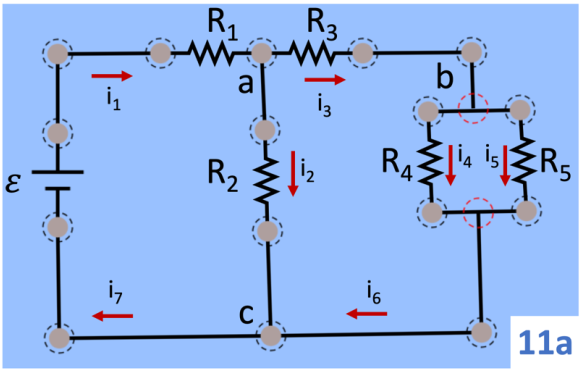
Esse circuito é razoavelmente complexo. Se o estudarmos detalhadamente você estará preparado para resolver a maioria dos circuitos do ENEM. Vamos supor que a fem, ε, da bateria seja 10 V, e que todas as resistências sejam iguais a 10 Ω. Vamos ver o que podemos dizer a respeito dos valores das correntes, sem fazer qualquer cálculo.
- i2 = i7, pelo princípio da conservação da carga, ou da corrente. Ou seja, a corrente que sai da bateria tem que ser a mesma que entra, não importa o circuito.
- Também pelo princípio da carga, I3 = i6.
- i4 = i5, porque as resistências são iguais e estão sob a mesma diferença de potencial. Mostre que essa conclusão é consequência da lei de Ohm, expressa na eq. (4.1).
- Os pontos a, b e c, onde a corrente se divide, são denominados nós.
- No nó a, a corrente i1 se divide em i2 e i3, de modo que i1 = i2 + i3 .
- No nó b, i3 se divide em i4 e i5, de modo que i3 = i4 + i5.
Transformando o procedimento descrito logo depois da eq. (4.4) em circuitos, e substituindo os valores da fem e das resistências, teremos os circuitos 11b-11e, a partir dos quais podemos calcular as correntes. A primeira pergunta é: neste circuito, que corrente é fornecida pela bateria? Esse cálculo é feito com o circuito 11e, quando todas as resistências foram substituídas pela resistência equivalente do circuito. Usando a eq. (4.1) no circuito 11e, obtém-se a corrente fornecida pela bateria, que é 0,63 A. Preste atenção, se o circuito fosse diferente, a corrente também seria diferente. A única coisa que permanece igual é a fem da bateria, 10 V.
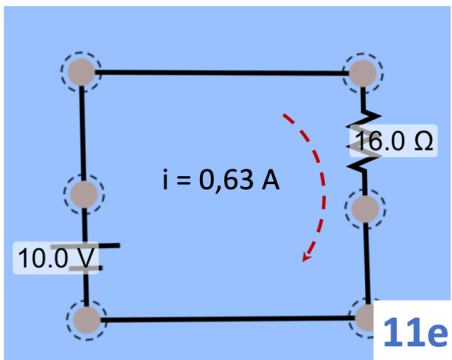
Agora vamos para o circuito 11b.
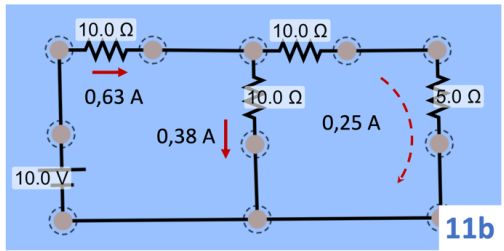
Veja que neste circuito as resistências R4 e R5, que estavam em paralelo no circuito original (11a), foram substituídas pela resistência de 5 Ω. Faça o cálculo e comprove que este é o valor correto. A corrente que sai da bateria, 0,63
A, é dividida em duas: 0,63 = 0,38 + 0,25. Como calculamos essas duas correntes? Transformando o circuito 11b no 11c, somando as resistências de 10 Ω e 5 Ω, que estão em série em 11b.
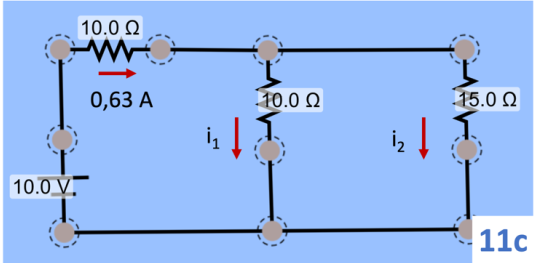
Agora precisamos fazer um cálculo um pouco mais elaborado. Veja que em 11c as resistências de 10 Ω e 15 Ω, estão em paralelo. Portanto, estão submetidas à mesma diferença de potencial. Usando a eq. (4.1), obtém-se:
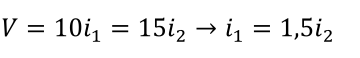
Por outro lado,
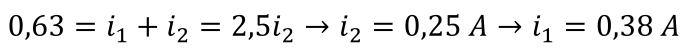
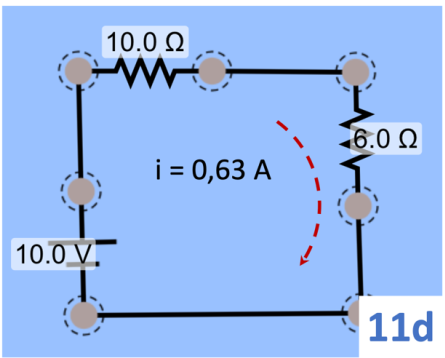
Finalmente, o circuito 11c é transformado no 11d, quando substituímos as resistências de 10 Ω e 15 Ω, estão em paralelo, pela resistência equivalente de 6 Ω.

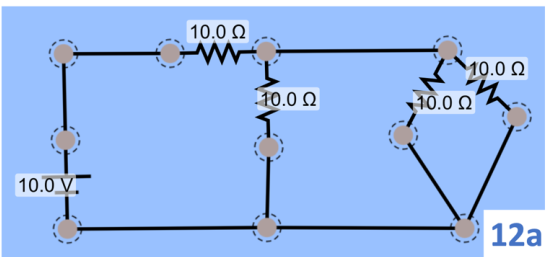
Vamos retirar a resistência R3 no circuito 11a, para você ficar convencido de que a bateria não é uma fonte de corrente constante. Ela é uma fonte de força eletromotriz constante. A corrente que ela fornece depende do circuito que ela alimenta. Agora o circuito 11a será substituído pelo circuito 12a.

Veja que o circuito 12a é idêntico ao circuito 11a, excetuando a resistência R3 que foi eliminada. Ele apenas está desenhado um pouco diferente. Repita os procedimentos apresentados para os circuitos 11 e mostre que agora, no circuito final, a resistência equivalente é 13,33 Ω, e que a corrente fornecida pela bateria é 0,75 A.
